Trực tâm là gì? Trực tâm của tam giác là giao điểm của ba đường cao tương ứng với ba đỉnh của tam giác đó. Đây là kiến thức cơ bản trong hình học mà chúng ta học trong chương trình toán học ở trung học cơ sở. Tuy nhiên, sau một thời gian, ít người vẫn nhớ chính xác điều gì là trực tâm. Vậy, trực tâm là gì? Hãy cùng Kiến Thức Live theo dõi bài viết dưới đây để hiểu rõ hơn về khái niệm này.
Trực tâm là gì?

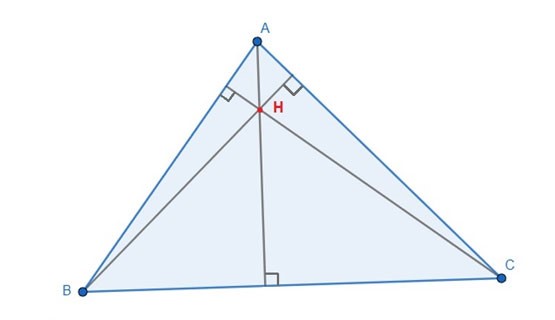
Trực tâm là điểm giao nhau của ba đường cao tương ứng với ba đỉnh của tam giác. Mỗi tam giác chỉ có duy nhất một trực tâm. Trực tâm có thể nằm bên trong hoặc bên ngoài tam giác.
Đường cao từ một đỉnh của tam giác là đường thẳng nối đỉnh đó tới cạnh đối diện và vuông góc với cạnh đối diện tại điểm giao nhau. Cạnh đối diện còn được gọi là cạnh đáy tương ứng với đường cao đó. Chiều dài đường cao chính là khoảng cách từ đỉnh đến cạnh đáy tương ứng với nó.
Giả sử tam giác LMN có ba đường cao lần lượt là LP, MQ, NI. Gọi S là giao điểm của ba đường cao đó, thì S chính là trực tâm của tam giác LMN.
Tính chất của trực tâm trong tam giác
Trực tâm của tam giác mang đến nhiều định lý và tính chất quan trọng. Để giải quyết các bài toán hình học hiệu quả, cần hiểu rõ những tính chất này và áp dụng chúng một cách nhanh chóng và chính xác.
Nếu ba đường cao của tam giác cùng đi qua một điểm, thì điểm đó được gọi là trực tâm của tam giác. Khoảng cách từ tâm đường tròn ngoại tiếp tam giác đến trung điểm của một cạnh bằng 1/2 khoảng cách từ trực tâm đến đỉnh còn lại của tam giác đó.
- Trong tam giác cân, đường trung trực tương ứng với cạnh đáy cũng là đường phân giác, đường cao và đường trung tuyến của tam giác đó.
- Trong tam giác mà đường trung tuyến cũng là đường phân giác, tam giác đó là tam giác cân.
- Trong tam giác mà đường trung tuyến cũng là đường trực tâm, tam giác đó là tam giác cân.
- Trực tâm của tam giác nhọn ABC trùng với tâm đường tròn nội tiếp tam giác, được xác định bởi ba đường cao tương ứng với ba đỉnh của tam giác ABC.
Định lý Carnot: Đường cao từ một đỉnh của tam giác cắt đường tròn ngoại tiếp tam giác sẽ tạo ra một điểm đối xứng với trực tâm của tam giác đó qua cạnh đáy đối xứng với đỉnh.
Ví dụ: Cho tam giác ABC có đường cao AH cắt đường tròn ngoại tiếp tam giác ABC tại D, trực tâm là điểm P.
Theo định lý Carnot, D đối xứng với P qua BC, Kết quả: Trong tam giác đều ABC, trọng tâm, trực tâm, điểm tâm đường tròn ngoại tiếp và điểm tâm đường tròn nội tiếp trùng nhau. Ví dụ: Tam giác đều ABC có đường cao đồng thời là đường trung tuyến và đường phân giác. Trực tâm O cũng là tâm đường tròn ngoại tiếp và tâm đường tròn nội tiếp.
Từ những tính chất trên, suy ra hệ quả: Trong tam giác đều, trực tâm, trọng tâm, tâm nội tiếp, điểm nằm trong tam giác, cách ba đỉnh và ba cạnh một cách đều, bốn điểm này cùng trùng nhau, tạo thành một điểm.
Cách xác định trực tâm trong tam giác
Khái niệm trực tâm là gì?Theo định nghĩa, trực tâm tam giác là điểm giao của 3 đường cao tương ứng với 3 đỉnh của tam giác. Tuy nhiên, chỉ cần tìm giao điểm của 2 đường cao cũng đủ để xác định trực tâm tam giác mà không cần phải vẽ cả 3 đường cao. Vị trí của trực tâm trong tam giác sẽ thay đổi tùy thuộc vào loại tam giác.
Trong tam giác nhọn, trực tâm sẽ nằm bên trong tam giác. Trong tam giác tù, trực tâm sẽ nằm bên ngoài tam giác. Còn trong tam giác vuông, trực tâm chính là đỉnh góc vuông của tam giác đó.
Ví dụ, trong tam giác vuông FHG với góc vuông tại H, điểm H cũng chính là trực tâm của tam giác.
Ngoài ra, từ những định lý và tính chất đã đề cập ở phần trước, chúng ta có thể xác định trực tâm tam giác bằng một số cách sau:
Theo tính chất: “Khoảng cách từ tâm đường tròn ngoại tiếp tam giác tới trung điểm của một cạnh bằng ½ khoảng cách từ trực tâm tới đỉnh còn lại của tam giác”, ta có thể dùng tâm đường tròn ngoại tiếp tam giác để xác định trực tâm như sau: Kẻ 1 đường cao và 1 đường từ tâm đường tròn này tới trung điểm của cạnh đối diện cùng với đỉnh của đường cao đó. Sau đó, tìm 1 điểm trên đường cao, cách đỉnh tam giác tương ứng một khoảng gấp đôi khoảng cách từ tâm đường tròn tới trung điểm cạnh đối diện, điểm đó chính là trực tâm.
Theo Định lý Carnot: Đường cao từ một đỉnh của tam giác cắt đường tròn ngoại tiếp tam giác tại một điểm, thì điểm ấy chính là điểm đối xứng với trực tâm tam giác qua cạnh đáy đối xứng với đỉnh đó. Ta cũng có thể xác định trực tâm như sau: Kẻ 1 đường cao của tam giác, đường cao đó cắt đường tròn tại một điểm thứ hai (nằm ngoài tam giác), sau đó tìm điểm đối xứng với điểm đó qua cạnh đáy chính là trực tâm.
Kết luận
Trên đây là một số chia sẻ của Kiến Thức Live về Trực tâm là gì và một số vấn đề liên quan. Nếu bạn đọc có bất kỳ câu hỏi hoặc thắc mắc nào, vui lòng chia sẻ trong phần bình luận bên dưới để chúng tôi hỗ trợ bạn ngay lập tức.